- inCAD Library Home
- > No.000260 Rotating and raising mechanism
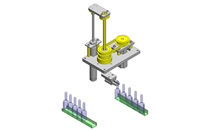
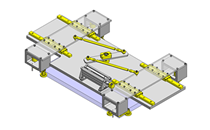
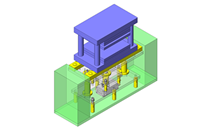
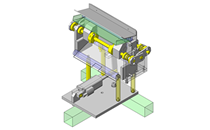
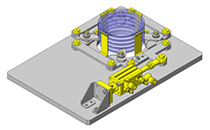
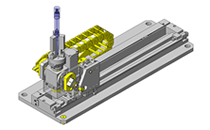
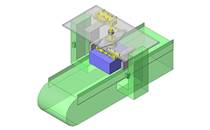
No.000260 Rotating and raising mechanism
35
35
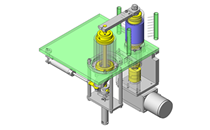
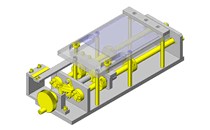
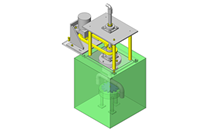
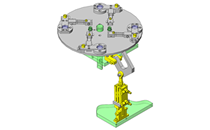
Lifting and rotating mechanism.
Related Category
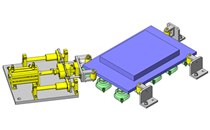
- * Unit assembly CAD data consists of some sub-assemblies.
Each sub-assembly unit can be used as it is or can be edited.
Application Overview
Purpose
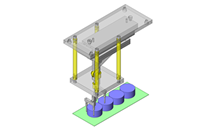
- Simplified multiple movement mechanism.
Points for use
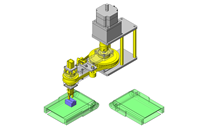
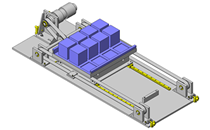
- Blower included within the cylindrical thin plastic work pieces serves as a cleaning mechanism.
- The work piece is raised into the fixed blower, at this point through the rotation and movement cleaning can be implemented from all angles of the work piece.
Target workpiece
- Long cylindrical workpiece.
- External dimension: Ø160 x H90mm
- Workpiece weight: 219g
Design Specifications
Operating Conditions or Design Requirements
- Specifications for workpiece operation
- Rotating angle: 360deg; Rotational speed: 0.5rev/sec = 3.14rad/sec
- Elevation stroke: 100mm; Elevation velocity: 100mm/sec
- Equipment dimensions
- External dimensions: W480 x D125 x H413mm
- Depth of underneath the table: 408mm
Required Performance
- Specifications for workpiece operation
- Rotation start time: 0.1sec
- Elevation start time: 0.1sec
Selection Criteria for Main Components
- Rotational torque of motor gear head.
- Thrust of cylinder.
Design Evaluation
Verification of main components
- Verification of the motor torque and cylindrical thrust required below.
- Rotational torque of motor gear head (60Hz)
- Rated rotational speed of motor: 1575 [Hz]→Gear head reduction ratio: (1575/60)/0.5 = 52.5 → 50 is adopted
- Starting torque of motor: 0.17N・m →Gear head conversion: 0.17 x 50 = 8.5N・m
- Allowable torque of gear head: 5.29N・m (from catalog) < 8.5 →5.29N・m is adopted
- Total inertia of rotating part: J = 6083kg・mm² = 6083 x 10-6kg・m²
- Rotation start time: 0.1sec → Rotation start angular acceleration: dω/dt = 3.14 / 0.1 = 31.4rad/sec²
- Required torque of rotating part: Tr = dω/dt x J = 31.4 x 6083 x 10-6 = 0.191N・m
- Belt overload coefficient Ks = 1.6 (catalog value), Required torque of driving side: 0.191 x 1.6 = 0.306N・m
- Safety factor: 5.29/0.306 = 17.3
- Thrust of cylinder
- Total weight of elevating part: 10.68kg, Acceleration for vertical push: g + dv/dt = 9.8 + 1 = 10.8m/sec²
- Required thrust of cylinder: F = 10.68 x 10.8 = 115.5N
- Operating pressure: 0.5MPa; Theoretical output of push side: 628N (from catalog)
- Safety factor: 628/115.5 = 5.44
- Specifications for workpiece operation
- Elevation start time: 0.1sec → Elevation start acceleration: dv/dt = 100 / 0.1 = 1000mm/sec² = 1m/sec²
Other Design Consideration
- Through the use of a timing pulley, the accuracy of the work piece angle can be improved.
- By separating the motor gear head and the rotating portion of the work piece, the overhang load of the gear head can be avoided.
Explore Similar Application Examples
Page
-
/
-